episode 2 episode 4

what is a convolution?

as an undergraduate student studying computer science, you are definitely required to take a few math courses during the first three or four semesters, ranging from calculus to linear algebra and differential equations, and you might've come across something called convolution theorem in laplace/z-transforms, which describes the product of said two transforms.

in this blog, i will describe a similar definition of convolution, under the context of deep learning, or specifically, convolutional neural networks (CNN).

databricks.com says:

convolution definition
sounds complicated and demotivating right? let's break it down.

cool math stuff.

convolution is simply the product of two matrices. one can imagine it as a relation [recall your jee math stuff], an input set and an output set. a sort of "mapping" is done between these two sets and the result is the output set.

don't take the set example too seriously, it's for your understanding.

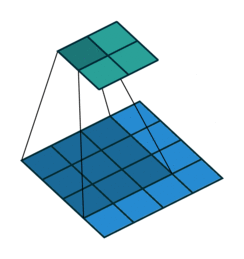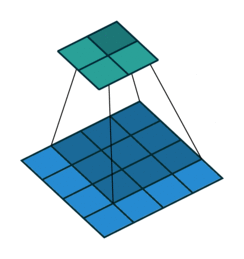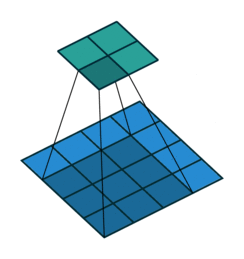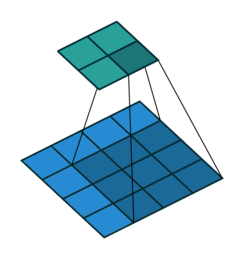
gif taken from here. convolution gif
consider the 'blue' matrix as the input matrix, and the 'green' as something known as a filter/kernel.

definition time.

kernel

filter

padding

stride

why do these definitions matter?

the input matrix, performs something called "element-wise multiplication" with the kernel in order to yield each element of the output matrix. this is different from the usual matrix multiplication done that involves a cross-product, where the rows of the input matrix is multipled with the columns of the kernel and is summed in the end.

there is a certain window within the input matrix that acts as a sub-matrix, and this window has the same dimensions as the kernel and each element of the window matrix is multiplied with each corresponding window of the kernel, and is finally summed up in the end, giving the first element of the output matrix.

though this article might be a bit mathy, it might help you understand it properly: article.

buzzwords and putting it all together.

when you came across convolutional neural networks, you might've come across something called downsampling, upsampling, etc. what it means is that:

upsampling

downsampling

where is convolution used?

mostly in image classification use-cases, these kernels actually have a special property: they contain information on the edges, and shapes. for example, if you are trying to classify a ball and a bat, then the kernel might have information on the edges of these objects and as the kernel is applied to the input matrix, the output matrix will contain information on the edges as well.

                
                    kernel = [[1, 0, -1], 
                              [1, 0, -1], 
                              [1, 0, -1]]

contains information on the "vertical edges" to pass through the input matrix, whereas a kernel like:

                
                    kernel = [[1, 1, 1], 
                              [0, 0, 0], 
                              [-1, -1, -1]]

contains information on the "horizontal edges" to pass through.

in reality however, these kernels are more complicated and through each layer, there's a different kernel that contains information on simple shapes, but as the layers increase, the model learns information and more complicated information, thanks to convolution.

the output equation is defined as follows: ((input_dim + 2 * padding - kernel) // stride) + 1

libraries like tensorflow or torch already provide convolution layers that could be implemented without doing so from scratch. however, it is important to get an understanding of how convolution works by understanding the math behind it.

convolution layers can be extended from lists to tensors. 2d convolution are the most commonly used layers for image processing but for certain cases in the medical sector or video-processing, one might require to use 3d convolutions for that matter.

how do i code this?

taken from here.

one can define a 2d convolution for example using just numpy, like so:

                
import numpy

class Conv2D: 
    def __init__(self, kernel: numpy.ndarray, stride: int, padding: int) -> None: 
        self.kernel = kernel
        self.stride = stride
        self.padding = padding

    def forward(self, in_matrix: numpy.ndarray) -> numpy.ndarray: 
        i_w, i_h = in_matrix.shape
        k_w, k_h = self.kernel.shape

        padded_input = numpy.pad(in_matrix, ((self.padding, self.padding), (self.padding, self.padding)), mode="constant", constant_values=0)

        o_h = ((i_h + 2*self.padding - k_h) // self.stride) + 1
        o_w = ((i_w + 2*self.padding - k_w) // self.stride) + 1

        out_matrix = numpy.ones((o_w, o_h))

        for i in range(o_w): 
            for j in range(o_h):
                o_i = i * self.stride
                o_j = j * self.stride

                i_end = o_i + len(self.kernel)
                j_end = o_j + len(self.kernel)

                sub_matrix = padded_input[o_i:i_end, o_j:j_end]
                out_matrix[i, j] = numpy.sum(numpy.multiply(sub_matrix, self.kernel))

        return out_matrix

you can take a look at my other pieces of code which i have written out in the repository linked above.

resources

here

krish naik